图像处理中的梯度和导数如何求?(Robert算子,Sobel算子,Prewitt算子,Laplace算子)

梯度的求法是多种多样的，根据不同的处理需要选择合适的算子(模版)。

1、水平垂直差分法

$ g(i,j) = |f(i,j)-f(i+1,j)| + |f(i,j)-f(i,j+1)| $

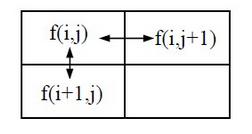
2、Robert 梯度算子

$ g(i,j) = |f(i,j)-f(i+1,j+1)| + |f(i+1,j)-f(i,j+1)| $

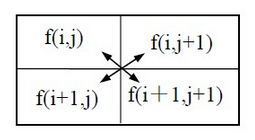
3、Sobel算子

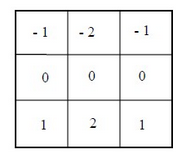
垂直方向

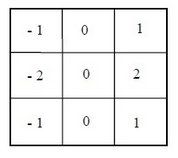
水平方向

4、Prewitt算子

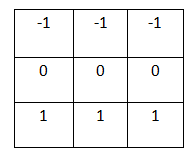
垂直方向

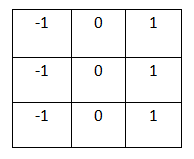
水平方向

5、拉普拉斯算子

$ g(i,j)=5 \times f(i,j) - |f(i-1,j)+f(i+1,j)+f(i,j-1)+f(i,j+1)| $

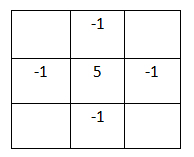
二阶差分的推导

对于数字图像 $f(i,j)$，利用差分方程对x和y方向上的二阶偏导数进行近似：
$$
\begin{equation}
\begin{split}
\frac{\partial^2 f}{\partial{x^2}} &= \frac{\partial(\Delta_x f(i,j))}{\partial x} = \frac{\partial(f(i+1,j)-f(i,j))}{\partial x} \
&= \frac{\partial f(i+1,j)}{\partial x} - \frac{\partial f(i,j)}{\partial x} \
&= f(i+2,j) -2f(f+1,j) + f(i,j)
\end{split}
\nonumber
\end{equation}
$$
上式以点$(i+1,j)$为中心，用i代换i+1可得以（i,j）为中心的二阶偏导数近似式：
$ \frac{\partial^2 f}{\partial x^2} = f(i+1,j)- 2f(i,j)+f(i-1,j) $
同理可得：
$ \frac{\partial^2 f}{\partial y^2} = f(i,j+1)-2f(i,j)+f(i,j-1) $
进而推出：
$ \frac{\partial^2 f}{\partial x \partial y} = \frac{\partial^2 f}{\partial y \partial x} = f(i+1,j+1)+f(i,j)-f(i,j+1)-f(i+1,j) $