旋转变换公式的推导：如下图，在2维坐标上，有一点$p(x, y)$，直线op的长度为r，直线op和x轴的正向的夹角为a。直线op围绕原点做逆时针方向b度的旋转，到达$p'(s,t)$

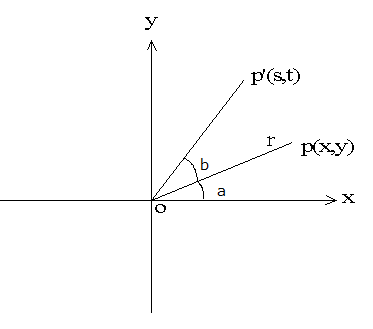
则有 $ s = r cos(a+b) = r cos(a) cos(b) - r sin(a) sin(b) \tag{1.1} $ $ t = r sin(a+b) = r sin(a) cos(b) - r cos(a) sin(b) \tag{1.2} $ 其中$x = r cos(a)$， $y = r sin(a)$ 代入(1.1), (1.2) ，得 $ s = x cos(b) - y sin(b) \tag{1.3} $ $ t = x sin(b) + y cos(b) \tag{1.4} $ 用行列式表示如下 $$ \left( \begin{array}{c} s \ t \end{array}

\right)

\left( \begin{array}{cc} cos(b) & -sin(b) \ sin(b) & cos(b) \end{array} \right) \left( \begin{array}{c} x \ y \end{array} \right) $$

用到的一些OpenCV中的函数：

CvMat*cv2DRotationMatrix(CvPoint2D32f center, double angle, double scale, CvMat*map_matrix);
                         Mat getRotationMatrix2D(Point2f center, double angle, double scale );

说明：计算旋转加缩放的仿射矩阵
参数：
- center：旋转中心
- angle：旋转度数，正值表示逆时针旋转。
- scale：各方向同性的缩放尺度
- map_matrix：输出参数，仿射变换矩阵，浮点型2*3矩阵
返回值：仿射变换矩阵
注意：默认的变换是以相反的顺序进行的，即从目标到源。对于目标图像中的任一点(x,y)，先计算出它在源图像中的坐标，再将此点的像素值拷贝到目标图像中，所以计算出的变换矩阵是从目标到源的变换矩阵。

例如逆时针旋转30度，不做缩放，计算出的变换矩阵为： $$ \left( \begin{array}{ccc} 0.866025, &0.5, &-91.5064 \ -0.5, &0.866025, &158.494 \end{array} \right) $$

void cvWarpAffine(const CvArr* src,CvArr* dst, const CvMat* map_matrix,
                  intflags=CV_INTER_LINEAR+CV_WARP_FILL_OUTLIERS, CvScalar fillval=cvScalarAll(0) );
void warpAffine(InputArray src, OutputArray dst, InputArray M, Sizedsize, int flags=INTER_LINEAR,
                int borderMode = BORDER_CONSTANT, constScalar& borderValue=Scalar() );

说明：对图像做仿射变换
参数：
- M：输入参数，2×3的仿射变换矩阵
- dsize：输出图像的尺寸
- flags：差值方法，若设置WARP_INVERSE_MAP标识，指明M是目的到源的变换。
- borderMode：边界处理方法
注意：当设置标志位WARP_INVERSE_MAP时，目标图像的计算公式为：$ dst(x,y)=src(M_{11}x+M_{12}y+M_{13}, M_{21}x+M_{22}y+M_{23}) $ 否则，先调用invertAffineTransform()计算出M的逆仿射变换M'，然后将M'带入以上公式进行变换。

#include<iostream>
#include<opencv2/imgproc/imgproc.hpp>
#include<opencv2/highgui/highgui.hpp>

using namespace std;
using namespace cv;

#define SCALE 0.5   //缩放比例

int main()
{
    Mat src = imread("pic3.png");
    Mat dst;//输出图像

    int angle = 30;//旋转角度(正值表示逆时针旋转)

    int length;//输出图像的宽度或高度
    //为了保证无论如何旋转都能放下，输出图像的长和宽都设为输入图像对角线长度乘以SCALE
    //但如果是缩小(SCALE<=1)，这样会导致临时图像中放不下原图，所以对于所有缩小的情况，输出图像和临时图像的长宽都设为原图的对角线长度
    if(SCALE <= 1)
        length = sqrt(src.cols*src.cols + src.rows*src.rows);
    else
        length = sqrt(src.cols*src.cols + src.rows*src.rows) * SCALE;
    //建立临时图像，长宽都是源图像的对角线长度，将源图像复制到临时图像的中心后再变换
    Mat tempImg(length,length,src.type());//临时图像，大小和输出图像一样大
    int ROI_x = length/2 - src.cols/2;//ROI矩形左上角的x坐标
    int ROI_y = length/2 - src.rows/2;//ROI矩形左上角的y坐标
    Rect ROIRect(ROI_x,ROI_y,src.cols,src.rows);//ROI矩形
    Mat tempImgROI2(tempImg,ROIRect);//tempImg的中间部分
    src.copyTo(tempImgROI2);//将原图复制到tempImg的中心

    Point2f center(length/2,length/2);//旋转中心
    Mat M = getRotationMatrix2D(center,angle,SCALE);//计算旋转的仿射变换矩阵

    //输出看看算出的矩阵是什么
    cout<<"变换矩阵："<<endl;
    cout<<M.at<double>(0,0)<<","<<M.at<double>(0,1)<<","<<M.at<double>(0,2)<<","<<endl;
    cout<<M.at<double>(1,0)<<","<<M.at<double>(1,1)<<","<<M.at<double>(1,2)<<","<<endl;

    warpAffine(tempImg,dst,M,Size(length,length));//仿射变换

    //显示
    imshow("src",src);
    imshow("tempImg",tempImg);
    imshow("dst",dst);

    waitKey(0);
    return 0;
}

效果图：

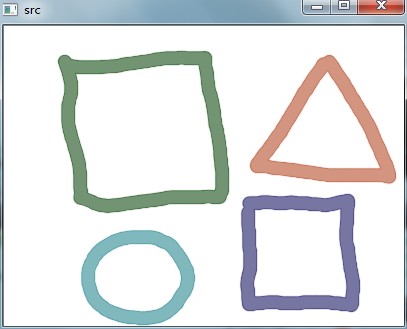
原图

临时图像1

结果1

临时图像2

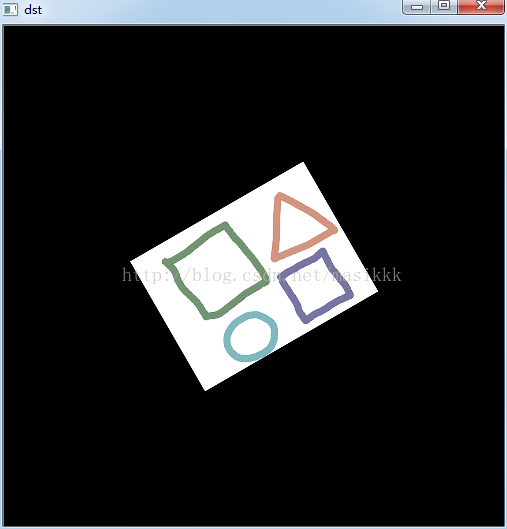
结果2